
It is Monday morning at 9:30 am. A selling order is placed on the exchange. Immediately after, two buying orders arrive for it. But there can only be one buyer. Who was faster and is eligible? How is fairness assured, and guaranteed without any risk of collision?
The trading of shares determines the actions on the stock market. The recording of trading events follows strict rules. The compliance of MiFID II organized by ESMA has created these to regulate the functionality of timestamps and therefore full integrity in trading.
Figure 1 shows the scenario described above with simplified figures. According to this, the selling order was made at a specific time, and it will normalize other points of time for relative events. Buying order 1 came at time 100 ms later and buying order 2 came at time 110 ms later. 10 ms seconds separate the two potential buyers. We see: Milliseconds play an extremely important role here.
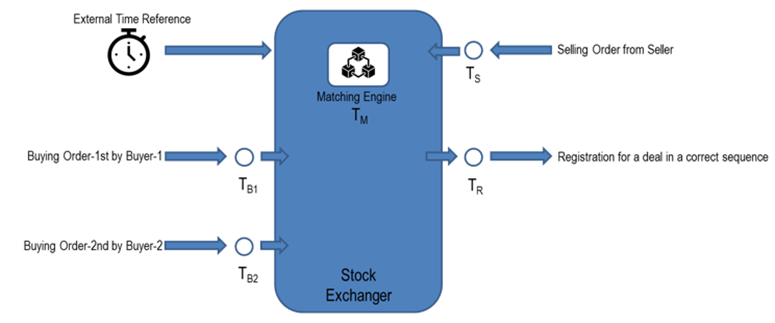
Accurate clocks are needed to ensure the correct sequence of purchases. With a difference of 10 ms from two buying orders and a possible error of +/-5 ms due to the uncertainty of clocks, in the “worst” case we end up with a purchase time of 105 ms each. Now so-called timestamps come into play. These are used to assign a unique time to an event. So, there would be an injustice if the error of the timestamps is longer than +/- 5 ms. However, according to MiFID II, the clocks of the devices involved in the trading venues, that will deal with the transaction of high-frequency algorithmic trading, must be synchronized to UTC time with a divergence less than 100 microseconds, and the granularity be 1 microsecond or better.
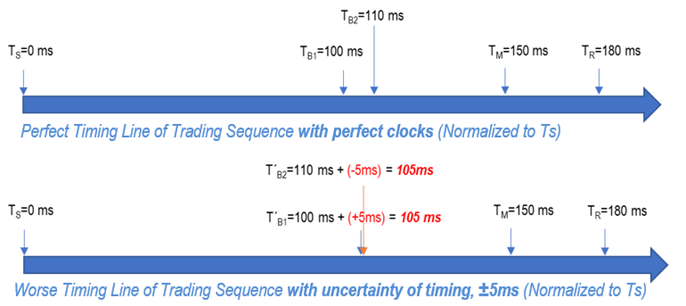
This leads us to the question:
How can timing errors be minimized in a system?
Figure 3 shows an exemplified timing signal route in an ideal case: the UTC clock is the starting point. The signal from this clock is sent to the Grand Master Clock via GNSS satellites. From here, the signal goes to Boundary Clocks and then to various hosts with Transparent Clocks. Inside a host machine, a basic causality relationship of processing an event among tasks should be satisfied. From the figure, we know:
- T1 is the task timing of detecting an event in an interface card.
- T2 is the task timing of receiving the event.
- T3 is the task timing of dealing with the event.
- T4 is the task timing for answering the event.
- T5 is the task timing for sending out an answer for the event through an interface card.
Synchronized clocks in the host machine should have a certain level of accuracy to retain a correct causality relationship, it means T1 < T2 < T3 < T4 < T5 must be kept true. From a higher-level point of view, among host machines in a network would naturally possess a more complicated causality relationship so that normally the requirement of timing accuracy becomes stricter at the upper position of a network.
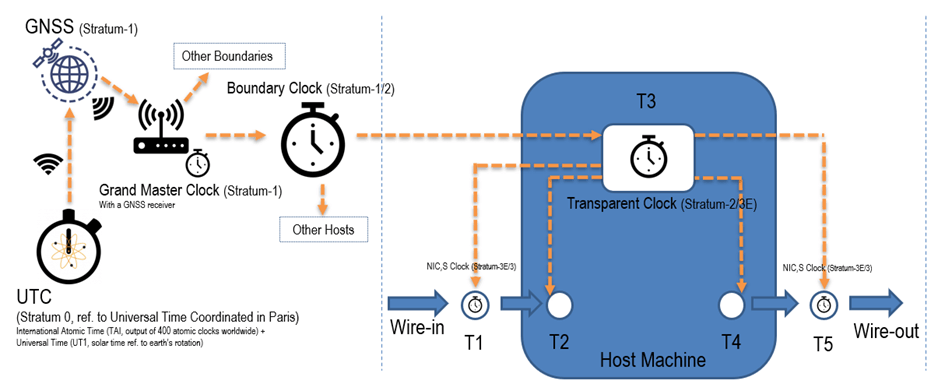
The whole thing takes place in a Precision Time Protocol (PTP, aka IEEE1588v2) network. PTP enables the synchronization of time settings of several devices in a computer network. There are several communicating clocks in a PTP network. The “Grandmaster Clock” gives the most accurate time and acts as a standard clock. An Ordinary Clock can be either the source as the master or the receiver of the time as the slave. These clocks synchronize directly. The Boundary Clock transports time information across a network boundary. A Transparent Clock improves the forwarding of time information within a network. It receives PTP messages and forwards them modified and corrected if necessary. The figure also shows the suggestions of the different stratum layers in different clocks. We will see what the numbers of Stratum mean in a moment.
The upper scenario describes the ideal state which the timing signal can be penetrated everywhere from up to bottom without any interruption and obstacle. But the reality is that synchronization is always limited due to GNSS’s vulnerability, packet transmission delays/disruptions, network congestion, or limited synchronization trigger intervals, etc.
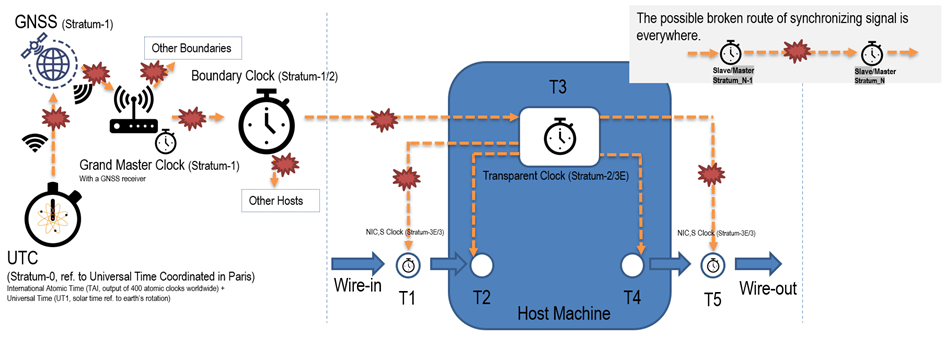
In order to continue sustaining the accuracy of the time and the time stamps, clocks in a PTP networks are needed to provide a precise time signal even in the event of a failure. Here, the holdover stability describes the capability of maintaining the clock integrity if the higher-level synchronization clocks are somehow lost or insufficient. A higher stratum layer means that the clock can survive a longer holdover duration and is associated with a more restrictive discipline so that it can tackle synchronization at a higher level.
How are the stratum layers defined?
According to the requirements of GR-1244 Core, there are comprehensive parameter sets defined for the different strata. For the most common grade Stratum 3 in PTP applications, there are two key parameters for a compliant oscillator in a synchronized clock. They are the Holdover Stability for 24 hours of +/-370 ppb involving the variation of temperature and daily aging and a Frequency Accuracy in Free Running of +/- 4.6 ppm including the 20-year aging and all causes from temperature, supply voltage, and load variation.

Our new JTS oscillator series of (VC)TCXOs with HCMOS or clipped sinewave is ideally suited for use in applications that require the Stratum 3 standard. It guarantees the corresponding values in Holdover Stability and Frequency Accuracy. If it is necessary, more specific performance indicators like MTIE and TDEV/ADEV can also be addressed through our technical support team with verification experiments in our own dedicated lab.
Do you need technical support or do you have questions about your frequency control component? Feel free to contact us.


 Deutsch
Deutsch 



