Frag die Technik: Wie dick ist eine Quarzscheibe von 40 MHz?

Wir starten in diesen Blogbeitrag mit einem kleinen Quiz:

Wie dick ist eine Quarzscheibe von 40 MHz? So dick wie…

• A: ein Fingernagel
• B: ein normales Blatt Druckerpapier
• C: ein Haar

Raten Sie für sich mit – die Auflösung kommt dann im Text. Starten wir zunächst aber einen Blick auf die Theorie:

Allgemein gilt: Zwischen der Resonanzfrequenz einer Quarzscheibe (auch Blank genannt) und der Dicke eines Quarzblättchen gibt es einen umgekehrt proportionalen Zusammenhang.

In anderen Worten – je höher die Resonanzfrequenz sein soll, desto geringer ist die dafür erforderliche Dicke dieses Quarzblanks. Dies liegt daran, dass sich zwischen den Grenzflächen der Quarzscheibe eine sogenannte stehende Welle ausbildet. Diese stehende Welle baut sich im Inneren des Quarzblättchens durch Reflexion an den beiden Grenzflächen der sich in Dickenrichtung ausbreitenden akustischen Querwelle auf. Die größte mechanische Verschiebung liegt in der Ebene des Quarzplättchens rechtwinklig zur Wellenausbreitungsrichtung.

Bei der Resonanzfrequenz passt eine ungerade Anzahl der halben akustischen Wellenlänge in die Dickenebene des Quarzplättchens. Daher ist die Dicke eines Quarzplättchens die hauptsächlich frequenzbestimmende Dimension der im AT-Schnitt hergestellten Quarze.

AT-Schnitt Quarze werden üblicherweise in den folgenden Frequenzbereichen hergestellt:

• 1 MHz ~ 60 MHz, Betrieb im Grundton-Modus
• 30 MHz ~ 250 MHz, Betrieb im Oberton-Modus (3.; 5.; 7.; 9. Oberton)

Wie bereits erwähnt, kann die erforderliche Dicke d eines Quarzplättchens abgeschätzt werden, da eine ungerade Anzahl von Halbwellenlängen in die Dickenebene des Quarzblanks passen sollte.

Zusätzlich zur Dicke des Quarzblanks muss die Ausbreitungsgeschwindigkeit v der akustischen Welle im Quarzmaterial berücksichtigt werden, um die Resonanzfrequenz f zu errechnen. Bei AT-Schnitt Quarzen beträgt die Ausbreitungsgeschwindigkeit v etwa 3320m/Sek. Darauf basierend kann die erforderliche Dicke d bei einer gegebenen Frequenz wie folgt abgeschätzt werden:

d ≈ n x ½ x v/f mit n = 1, 3, 5, …

Im Grundton-Modus ergeben sich folgende Dicken eines Quarzplättchens bei den Frequenzen 10,0 MHz und 40,0 MHz:

• 10,0 MHz ⇢ d = 166,0μm
• 40,0 MHz ⇢ d = 41,5μm

Bei einem Quarzblank mit einer Resonanzfrequenz von 40 MHz handelt es sich also um eine relativ dünne Scheibe. Sie hat eine Dicke von nur 41,5µm, was etwa 0,04 mm sind. Damit entspricht die Dicke etwa dem Durchmesser eines menschlichen Haares und ist ungefähr ein Zehntel der Dicke eines Blattes Papier. Richtig war also Antwort C 😊.

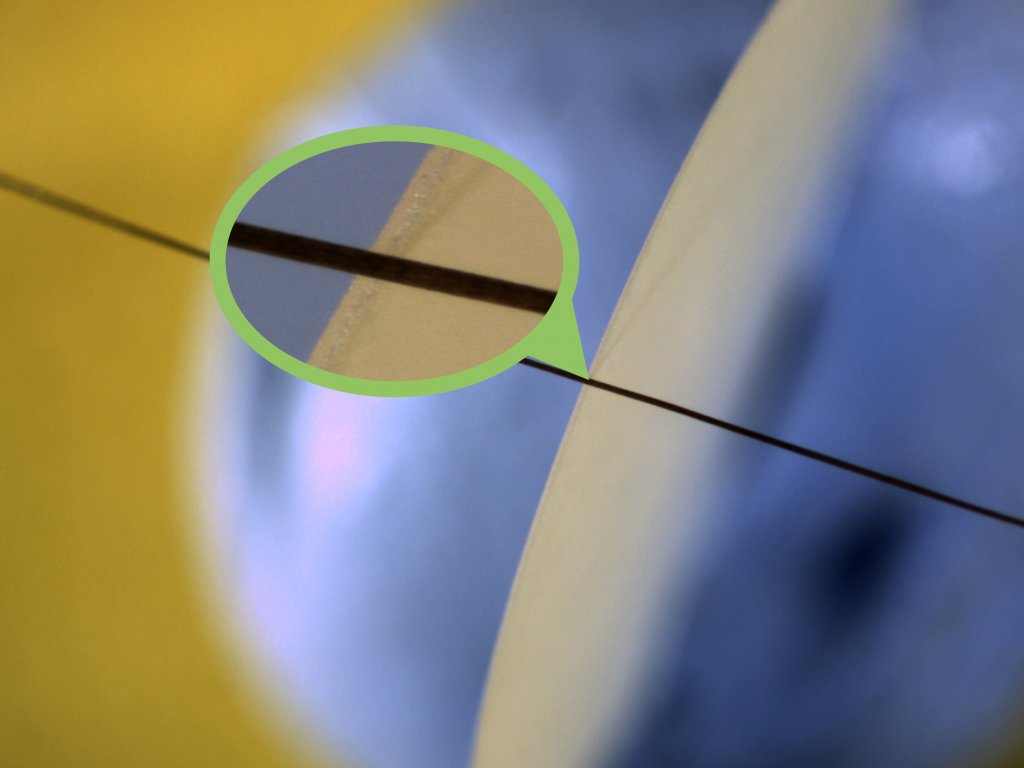
Damit Sie sich besser vorstellen können, wo auf dem Bild das Haar und wo das Quarzblank ist, haben wir hier noch einen Einblick in den Versuchsaufbau:

Und wie kann nun zum Beispiel sichergestellt werden, dass die Toleranz der Resonanzfrequenz nur um ±10 ppm (parts per million) von der gewünschten Resonanzfrequenz abweicht?

Auf die Nenn-Dicke der Quarzscheibe übertragen würde eine Abweichung der Resonanzfrequenz von ± 10 ppm einer Dickentoleranz von nur ± 0,415 nm entsprechen. Dies ist selbst mit ausgefeiltesten mechanischen Arbeitsschritten nicht erreichbar. Zudem soll ein Schwingquarz ein sehr preisgünstiges Bauelement sein, das auch im Consumer-Bereich eingesetzt werden soll.

Wie ist also diese geringe Frequenztoleranz von nur ± 10 ppm zu erreichen?

Anstelle der in der Praxis nicht erreichbaren mechanischen Toleranz wird ein Trick angewendet. Denn die Resonanzfrequenz der Quarzscheibe lässt sich in einem sehr geringen Bereich durch die Kopplung eines Zusatzgewichts beeinflussen. Um zu verstehen, wie dieser Trick funktioniert ist es wichtig zu wissen, dass die Quarzscheibe mit Hilfe zweier Elektroden zum Schwingen angeregt werden kann. Dies funktioniert nur aufgrund des piezoelektrischen Effekts, den wir an anderer Stelle mal erklären.

Die beiden Elektroden auf den sich gegenüberliegenden Oberflächen des Quarzblanks haben eine sehr geringe Masse, die zusätzlich zur Dicke des Blanks die Resonanzfrequenz beeinflussen. Aus diesem Grund wird die Quarzscheibe etwas dünner als rechnerisch ermittelt ausgeführt, da aufgrund der zusätzlichen gekoppelten Masse der Elektroden die Resonanzfrequenz etwas sinkt.

Nach Aufbringen der beiden Elektroden durch einen Sputterprozess sollte die resultierende Resonanzfrequenz noch knapp über der finalen Nennfrequenz liegen. Im letzten Fertigungsschritt vor dem hermetischen Verschluss des Quarzgehäuses erfolgt dann der eigentliche “Trick“.

Er besteht darin, noch eine extrem dünne weitere metallische Schicht auf die bestehende Elektrode aufzubringen. Dies erfolgt durch einen weiteren Sputterprozess, während kontinuierlich die Resonanzfrequenz der Quarzscheibe gemessen wird. Dieser zweite Sputterprozess erfolgt vergleichsweise langsam und wird gestoppt, sobald die exakte Nennfrequenz erreicht wird.

Durch diesen “Trick“ des gezielten und individuell gesteuerten Aufbringens einer ganz geringfügigen Zusatzmasse lässt sich die Resonanzfrequenz sehr präzise einstellen, wodurch eine Toleranz der Resonanzfrequenz von ± 10 ppm oder besser erreicht werden kann. Diese Präzision wäre durch rein mechanische Bearbeitungsschritte nicht erreichbar.

Haben Sie Fragen oder benötigen Sie Hilfe bei der Wahl des geeigneten Bauteils für Ihre Schaltung? Kontaktieren Sie uns gerne.